Hasse diagrams | Christoph Minz

A Hasse diagram is a graphical representation of a partially ordered set (a set with a transitive, reflexive, antisymmetric ordering), where all elements are drawn as vertices and edges (directed towards the top of the page) connect pairs of vertices x and y if x < y and there is no other element z such that x < z < y. Partially ordered sets (or posets for short) appear as an abstract structure in many areas of mathematics, though Hasse diagrams are mostly useful for finite posets.

In gravitational physics, a spacetime manifold is a poset where the ordering is given by its causal structure that partially orders the spacetime points (events). Their discrete analogous are lattices and causal sets (or causets for short), which are locally finite posets, so every set of elements z between a pair of events x < z < y is finite and thus representable with a Hasse diagram. Causal sets are the central objects in an approach to quantum gravity, where a spacetime manifold is considered to be the macroscopic counterpart to ensembles of causal sets at a microscopic level.

Below I give a brief introduction to some tools to create and type-set Hasse diagrams for posets and causal sets.

LaTeX package: causets

The LaTeX package causets (Minz, 2020) provides macros to type-set Hasse diagrams of partially ordered sets (posets) and causal sets (causets), and use them in graphics. It is available through CTAN, but if you have a recent full LaTeX installation, then it might be already installed on your system. For example, it is ready to use on Overleaf. Just load the package with

\usepackage{causets}

The package provides three main commands to show a diagram in text and math mode. The macros are

\pcauset{..,i,..} to insert a Hasse diagram of a 2D-order using a permutation of consecutive integers,
\rcauset{..,i,..}{..,i/j,..} to print a diagram based on a permutation as before (first argument) but with those links i/j that listed in the second argument removed,
\causet{..,i,..}{..,i/j,..} to place a diagram where the vertices are arranged according to a 2D-order permutation (first argument) but the links are added only between the element pairs i/j given in the second argument.

For example, use

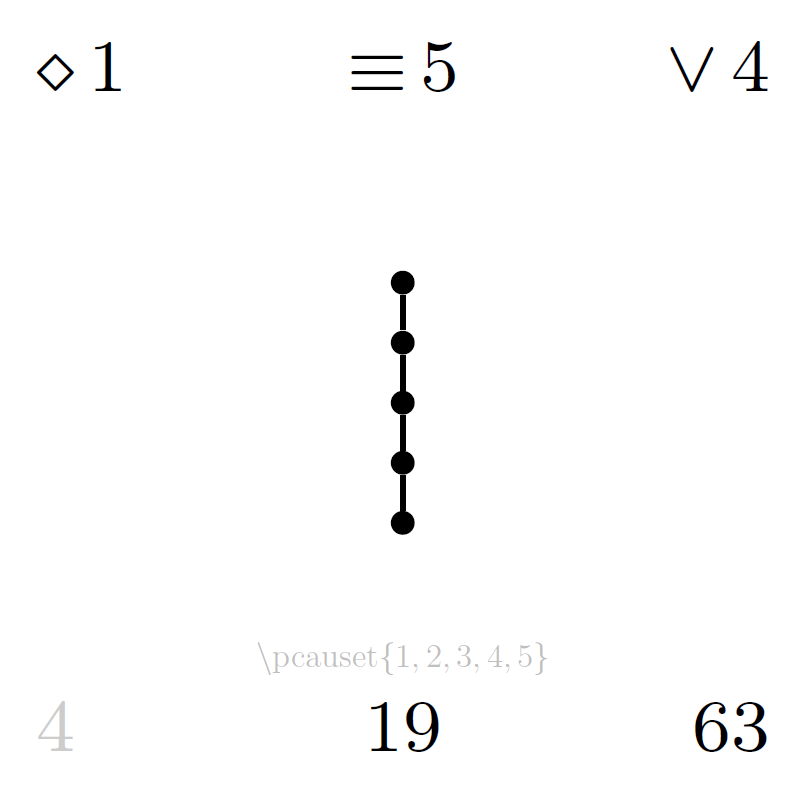
\pcauset{1,2,...,7}  % to insert a 7-chain
\pcauset{7,6,...,1}  % to insert a 7-antichain

The diagrams are type-set with TikZ, so that there are plenty of additional options to label, restyle, and combine the graphics with other TikZ code. You may find more information in the package manual via CTAN and the package repository on GitHub.

Online editor: PrOSET

The macros of the LaTeX package are built on integer permutations that determine the positions of the elements in the diagrams. To find a suitable permutation for a poset diagram while getting a live preview, I have developed the ‘PrOSET editor’:

Go to the PrOSET editor

Catalogue of finite posets

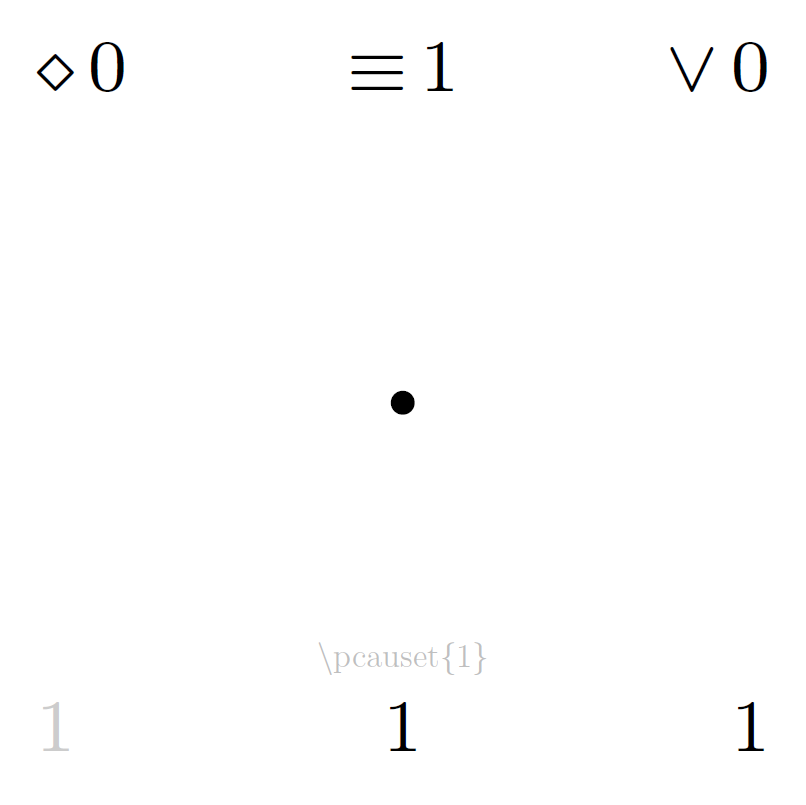
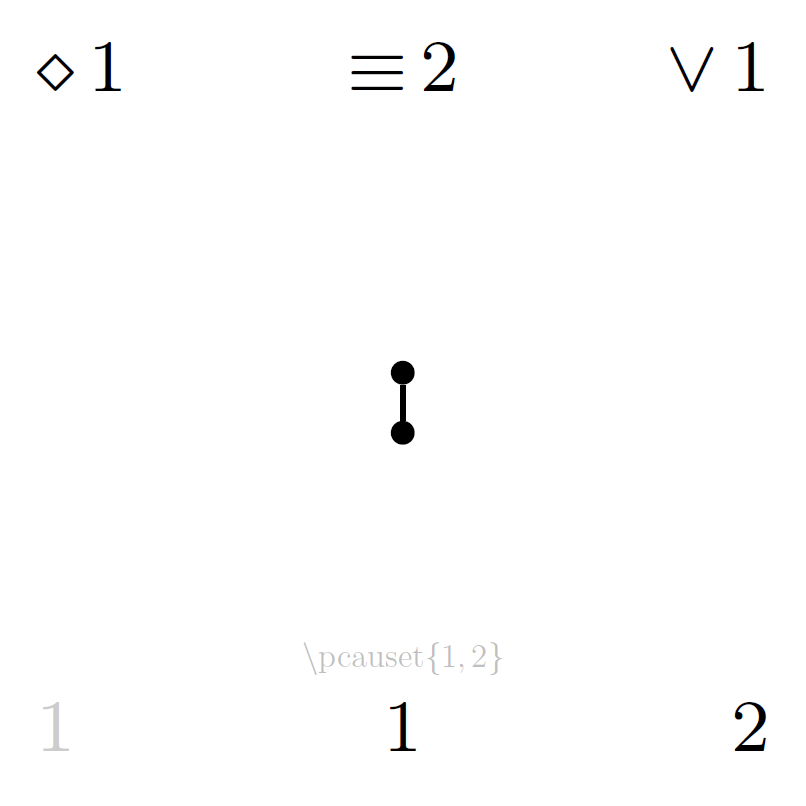
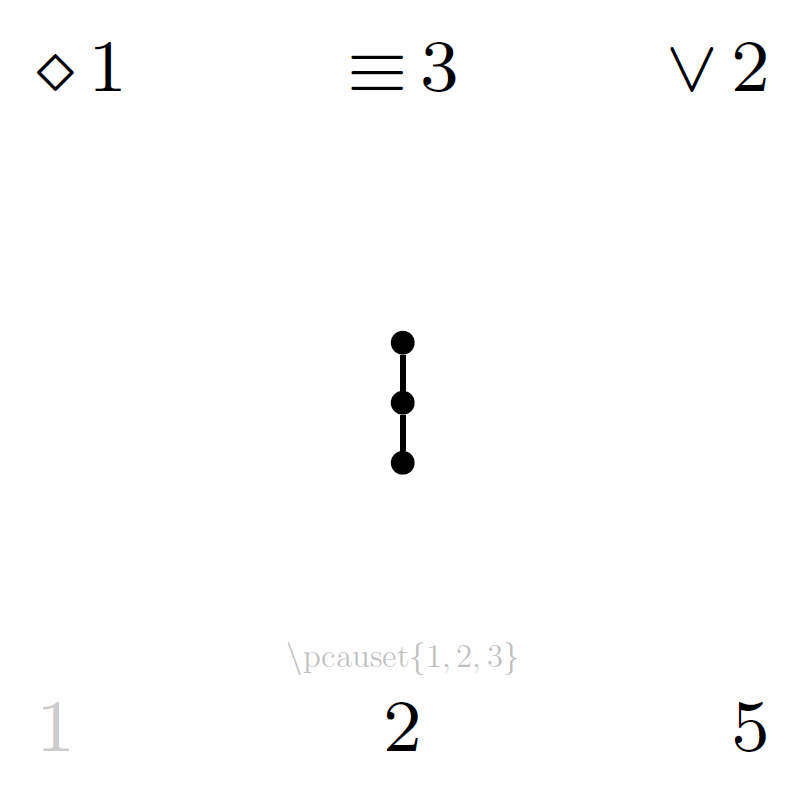
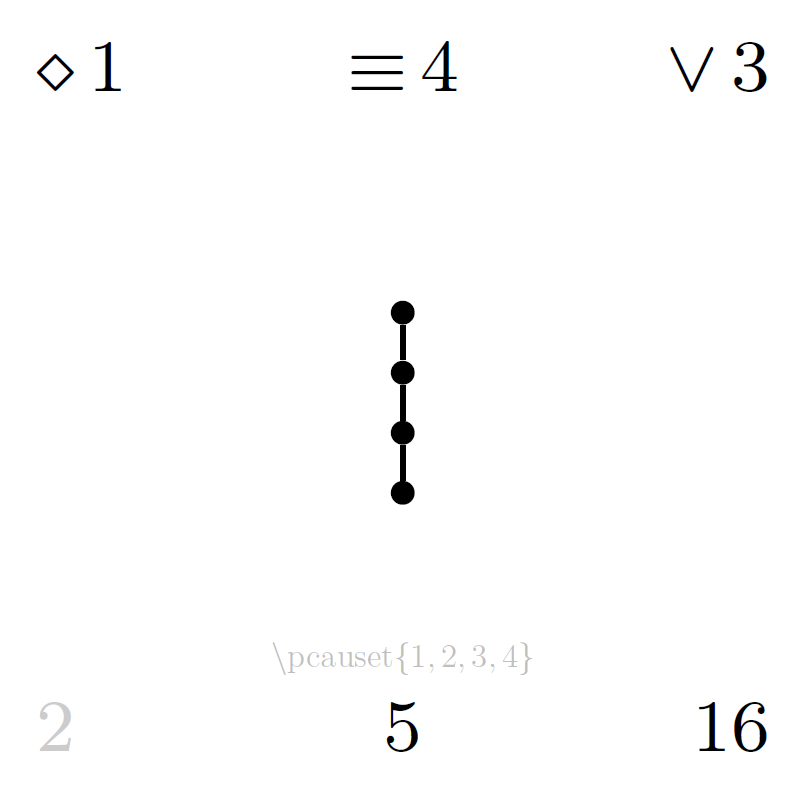
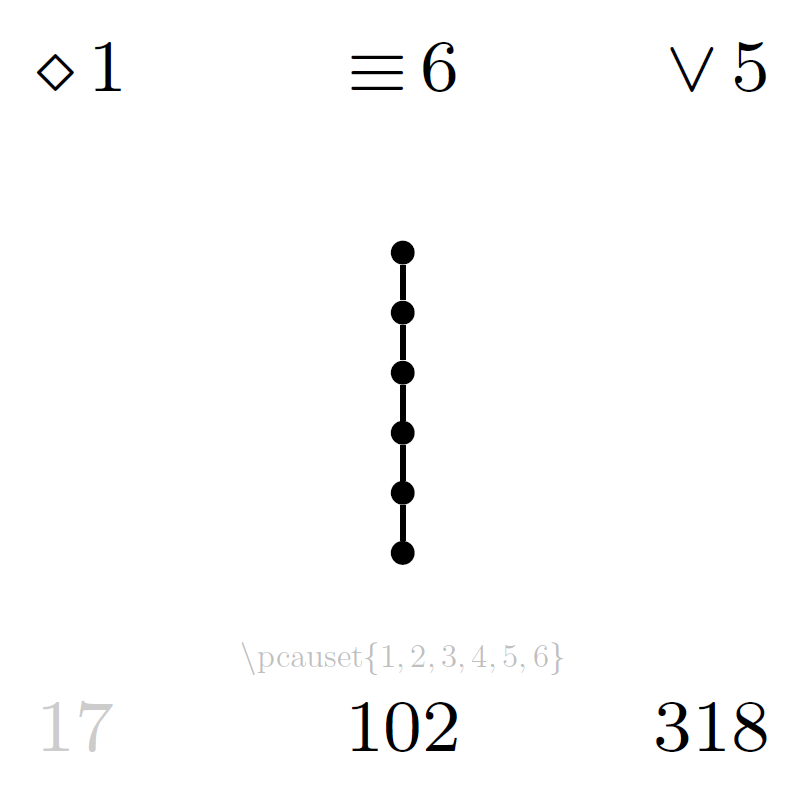
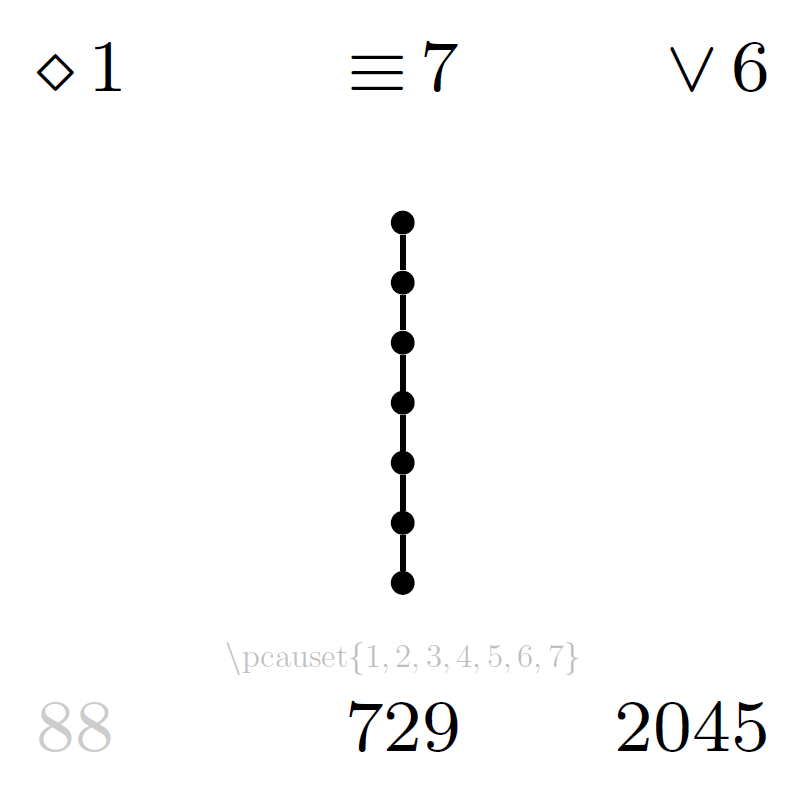
The following catalogue lists diagrams for all posets up to cardinality 6. The total number of distinct partial orders on sets of n elements (corresponding to the total page number of each part of the catalogue) is recorded in the OEIS as sequence A000112. All diagrams in the catalogue below are generated with the LaTeX package and the symmetry properties annotated in the catalogue are defined in (Minz, 2024).

Each file of the catalogue contains all partial orders on a given number of elements, one poset per page including the annotated properties:

upper left d: dimension of the order (as primary page order, descending)
upper centre l: number of layers (as secondary page order, ascending)
upper right e: number of edges in the diagram (as tertiary page order, ascending)
centre: Hasse diagram
lower left s: prime symmetry (1: singleton-symmetry, 2: 2-chain-symmetry, 3: wedge-symmetry, 4: vee-symmetry, 5: 3-chain-symmetry), or 1-stable locally unsymmetric poset counter
lower centre u: locally unsymmetric poset counter
lower right p: poset counter

Legend

Format and legend of each page in the catalogue, showing the diagram in the centre with the LaTeX macro below, as well as some properties in the corners of the page.

Posets with cardinality 1

The singleton is the only poset with cardinality 1, which is also locally unsymmetric.

Posets with cardinality 2

The file shows diagrams for the 2 posets with cardinality 2, where the 2-chain is locally unsymmetric.

Posets with cardinality 3

The file shows diagrams for all 5 posets with cardinality 3, including 2 locally unsymmetric posets.

Posets with cardinality 4

The file shows diagrams for all 16 posets with cardinality 4, including 5 locally unsymmetric posets.

Posets with cardinality 5

The file shows diagrams for all 63 posets with cardinality 5, including 19 locally unsymmetric posets.

Posets with cardinality 6

The file shows diagrams for all 318 posets with cardinality 6, including 102 locally unsymmetric posets.

Posets with cardinality 7

The file shows diagrams for all 2045 posets with cardinality 7, including 730 locally unsymmetric posets.

In case you spot an error in the catalogue, please get in contact with me.

Partially ordered sets (posets) have a universal appearance as an abstract structure in many areas of mathematics. Though, even their explicit enumeration remains unknown in general, and only the counts of all partial orders on sets of up to 16 unlabelled elements have been calculated to date, see sequence A000112 in the OEIS. In this work, we study automorphisms of posets in order to formulate a classification by local symmetries. These symmetries give rise to a division operation on the set of all posets and lead us to the construction of symmetry classes that are easier to characterise and enumerate. Additionally to the enumeration of symmetry classes, I derive polynomial expressions that count certain subsets of posets with a large number of layers (a large height). As an application in physics, I investigate local symmetries (or rather their lack of) in causal sets, which are discrete spacetime models used as a candidate framework for quantum gravity.

This LaTeX package uses TikZ to generate (Hasse) diagrams for causal sets (causets) to be used inline with text or in mathematical expressions. The macros can also be used in the tikzpicture environment to annotate or modify a diagram, as shown with some examples in the documentation.