Publications
List of my publications in reversed chronological order.
My publications are also listed on arXiv and on INSPIRE.
2025
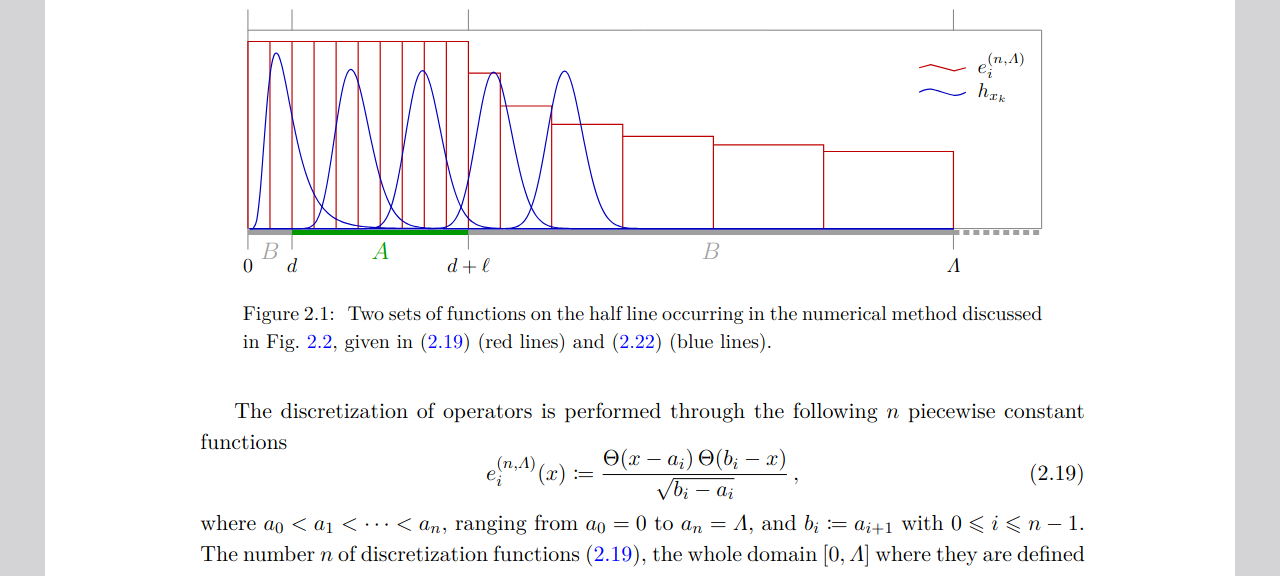
- Modular Hamiltonian of the massive scalar field on the half line: A numerical approachChristoph Minz and Erik TonniarXiv preprint, Dec 2025
We study the modular Hamiltonian of an interval for the ground state of a massive free scalar field on the half line with Robin boundary conditions, by employing a numerical method. When the interval is adjacent to the boundary, we find numerical evidence that the modular Hamiltonian is non-local, except for the limiting cases of the massless scalar satisfying either Dirichlet or Neumann boundary conditions. When the interval is separated from the boundary, the numerical analysis indicates that the modular Hamiltonian is non-local for all these boundary conditions and any value of the mass.
2024
- Do causal sets have symmetries?Christoph MinzIn 17th Marcel Grossmann Meeting: On Recent Developments in Theoretical and Experimental General Relativity, Gravitation, and Relativistic Field Theories, Oct 2024
Causal sets are locally finite, partially ordered sets (posets), which are considered as discrete models of spacetimes. On the one hand, causal sets corresponding to a spacetime manifold are commonly generated with a random process called sprinkling. This process keeps only a discrete set of points of the manifold and their causal relations (loosing the spacetime symmetries in each sprinkle). On the other hand, the main conjecture of causal set theory is that given an ensemble of causal sets there is a corresponding spacetime manifold and the continuum symmetries of it are like all manifold properties ’reconstructable’ from the partial orders of all the causal sets in the ensemble. But most generic finite posets have very few layers (’instances of time’) in contrast to sprinkles with many layers in a sufficiently large spacetime region. In a recent project, I investigated the automorphism groups of (finite) posets in order to identify and classify their symmetries systematically. The comparison of local symmetries of generic posets (including Kleitmann-Rothschild orders) with sprinkled causal sets may help us to find those posets that can serve as discrete spacetime models in causal set theory.
- Local symmetries in partially ordered setsChristoph MinzarXiv preprint, Jun 2024
Partially ordered sets (posets) have a universal appearance as an abstract structure in many areas of mathematics. Though, even their explicit enumeration remains unknown in general, and only the counts of all partial orders on sets of up to 16 unlabelled elements have been calculated to date, see sequence A000112 in the OEIS. In this work, we study automorphisms of posets in order to formulate a classification by local symmetries. These symmetries give rise to a division operation on the set of all posets and lead us to the construction of symmetry classes that are easier to characterise and enumerate. Additionally to the enumeration of symmetry classes, I derive polynomial expressions that count certain subsets of posets with a large number of layers (a large height). As an application in physics, I investigate local symmetries (or rather their lack of) in causal sets, which are discrete spacetime models used as a candidate framework for quantum gravity.
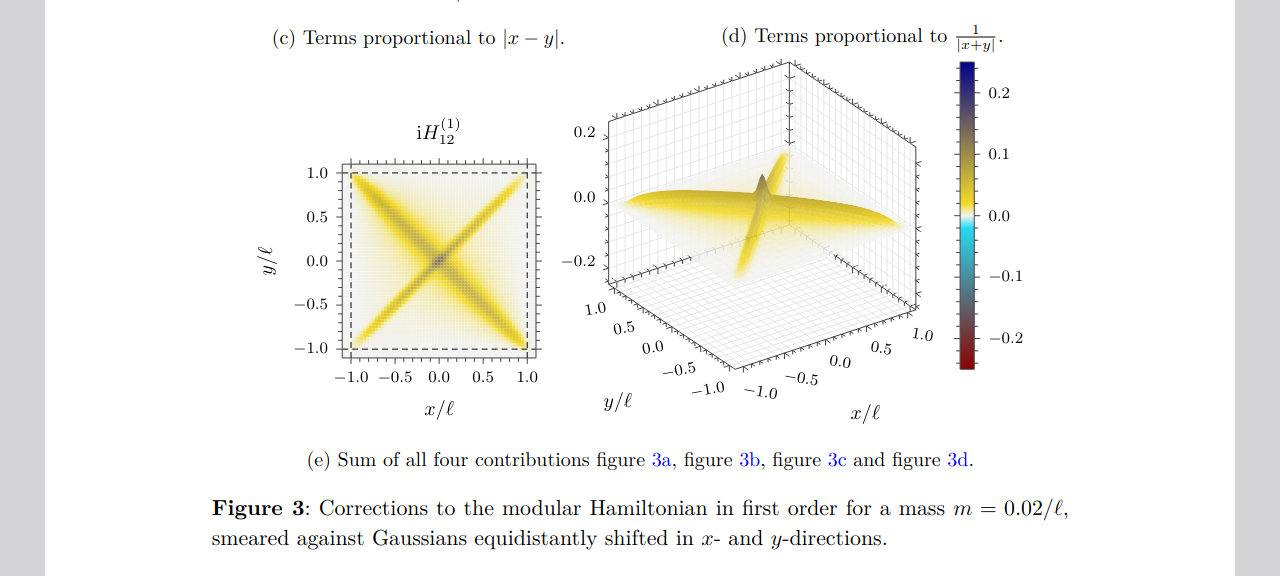
- Modular Hamiltonian for Fermions of Small MassDaniela Cadamuro, Markus B. Fröb, and Christoph MinzAnn. Henri Poincare, Dec 2024
We consider the algebra of massive fermions restricted to a diamond in two-dimensional Minkowski spacetime, and in the Minkowski vacuum state. While the massless modular Hamiltonian is known for this setting, the derivation of the massive one is an open problem. We compute the small-mass corrections to the modular Hamiltonian in a perturbative approach, finding some terms which were previously overlooked. Our approach can in principle be extended to all orders in the mass, even though it becomes computationally challenging.
@article{CadamuroFroebMinz:2024, author = {Cadamuro, Daniela and Fr\"ob, Markus B. and Minz, Christoph}, title = {{Modular Hamiltonian for Fermions of Small Mass}}, eprint = {2312.04629}, archiveprefix = {arXiv}, primaryclass = {hep-th}, doi = {10.1007/s00023-024-01508-0}, journal = {Ann. Henri Poincare}, month = dec, year = {2024}, } - Quantization, dequantization and distinguished statesEli Hawkins, Christoph Minz, and Kasia RejznerJ. Phys. A: Math. Theor., Sep 2024
Geometric quantization is a natural way to construct quantum models starting from classical data. In this work, we start from a symplectic vector space with an inner product and — using techniques of geometric quantization — construct the quantum algebra and equip it with a distinguished state. We compare our result with the construction due to Sorkin — which starts from the same input data — and show that our distinguished state coincides with the Sorkin-Johnson state. Sorkin’s construction was originally applied to the free scalar field over a causal set (locally finite, partially ordered set). Our perspective suggests a natural generalization to less linear examples, such as an interacting field.
@article{HawkinsMinzRejzner:2024, author = {Hawkins, Eli and Minz, Christoph and Rejzner, Kasia}, title = {{Quantization, dequantization and distinguished states}}, eprint = {2207.05667}, archiveprefix = {arXiv}, primaryclass = {math-ph}, doi = {10.1088/1751-8121/ad7427}, journal = {J. Phys. A: Math. Theor.}, volume = {57}, number = {39}, pages = {395205}, month = sep, year = {2024}, }
2023
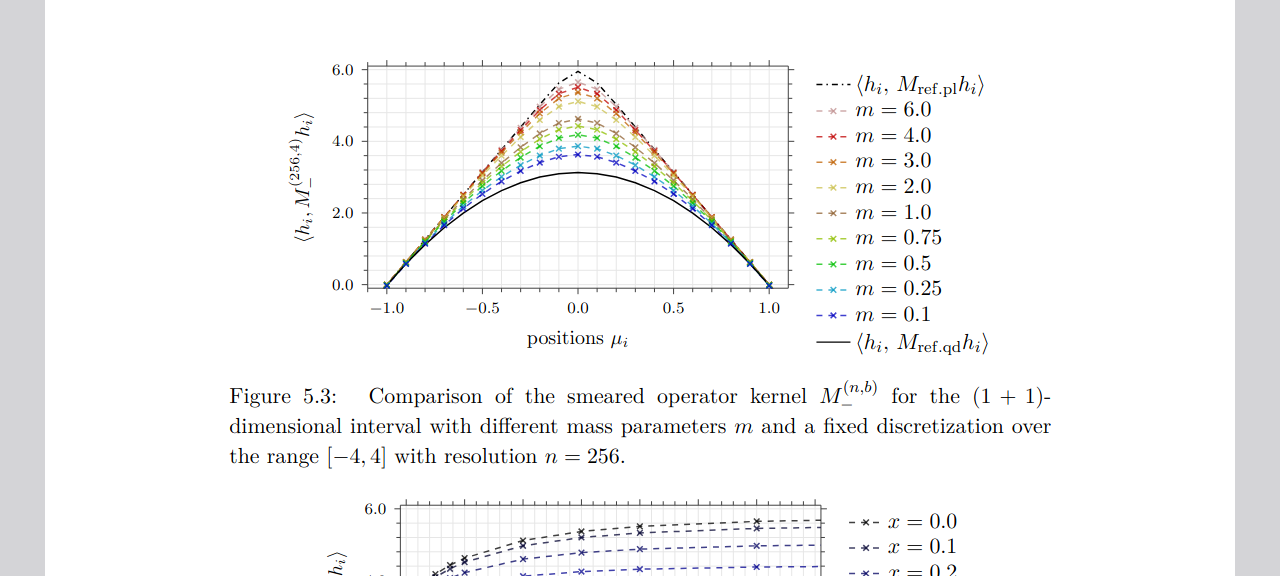
- On the Mass Dependence of the Modular Operator for a Double ConeHenning Bostelmann, Daniela Cadamuro, and Christoph MinzAnn. Henri Poincare, May 2023
We present a numerical approximation scheme for the Tomita-Takesaki modular operator of local subalgebras in linear quantum fields, working at one-particle level. This is applied to the local subspaces for double cones in the vacuum sector of a massive scalar free field in (1 + 1)- and (3 + 1)-dimensional Minkowski spacetime, using a discretization of time-0 data in position space. In the case of a wedge region, one component of the modular generator is well-known to be a mass-independent multiplication operator; our results strongly suggest that for the double cone, the corresponding component is still at least close to a multiplication operator, but that it is dependent on mass and angular momentum.
@article{BostelmannCadamuroMinz:2023, author = {Bostelmann, Henning and Cadamuro, Daniela and Minz, Christoph}, title = {{On the Mass Dependence of the Modular Operator for a Double Cone}}, eprint = {2209.04681}, archiveprefix = {arXiv}, primaryclass = {math-ph}, doi = {10.1007/s00023-023-01311-3}, journal = {Ann. Henri Poincare}, volume = {24}, number = {9}, pages = {3031--3054}, month = may, year = {2023}, }
2021
- Algebraic Field Theory on Causal Sets: Local Structures and Quantization MethodsChristoph MinzUniversity of York, Department of Mathematics, United Kindgom, Dec 2021uk.bl.ethos.844269
I investigate aspects of classical and quantum real scalar field theory on causal sets — a discrete framework for space and time — using the algebraic perspective. After reviewing and generalizing necessary notation, I consider different discretizations of the Klein-Gordon field equations to describe the dynamics of a scalar field. I generalize a recently proposed discretization method that uses a preferred past structure (which assigns a specific past element to every element of a causal set) to lattices in Minkowski spacetime of any dimension. With numerical techniques, I analyse criteria to assign a preferred past structure to more general causal sets that are generated via sprinkling — a Poisson process on a given spacetime manifold. It turns out that there exists a method that is very successful in selecting a preferred past uniquely with high probability (for finite causal sets on Minkowski spacetime). I review quantization methods and algebraic states. For the case of a finite causal set, I show how to construct a symplectic vector space with an inner product. The given structure lets me apply the method of geometric quantization to determine a quantum algebra and define a state, which is the Sorkin-Johnston state — commonly considered for quantum field theory on causal sets. Additionally, I discuss the relationship of the geometrically constructed quantum algebra to deformation quantization to motivate future applications like a non-perturbative construction of the quantum algebra for interacting field theories via geometric quantization.
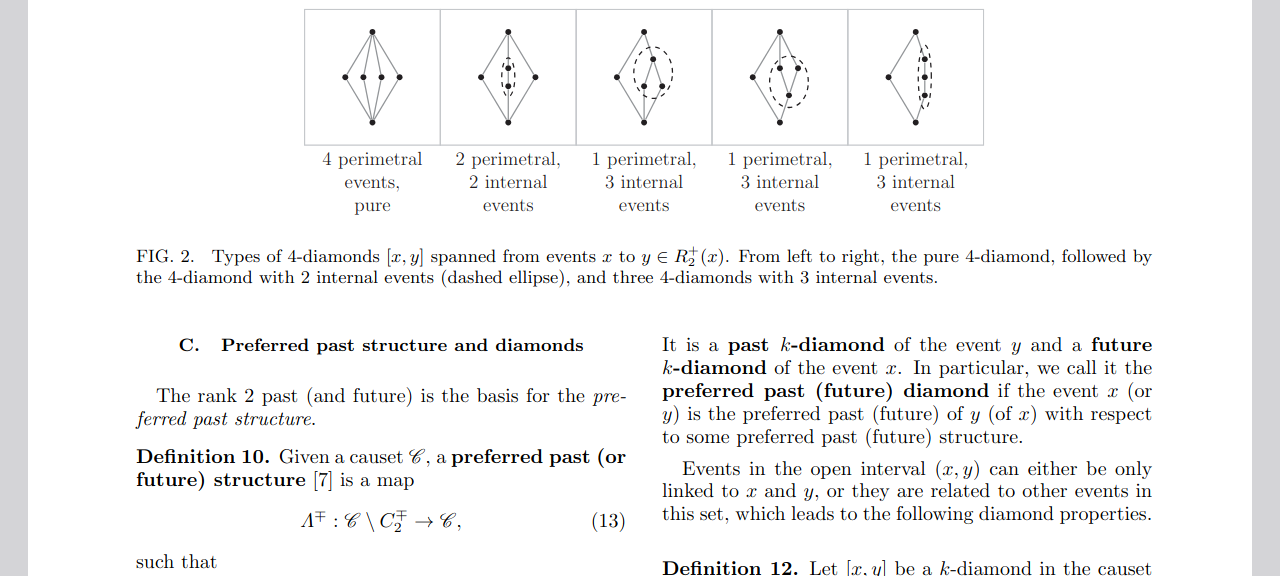
@phdthesis{Minz:2021, author = {Minz, Christoph}, title = {{Algebraic Field Theory on Causal Sets: Local Structures and Quantization Methods}}, school = {University of York, Department of Mathematics, United Kindgom}, note = {uk.bl.ethos.844269}, month = dec, year = {2021}, } - Local structure of sprinkled causal setsPhys. Rev. D, Aug 2021
We describe numerical and analytical investigations of causal sets sprinkled into spacetime manifolds. The first part of the paper is a numerical study of finite causal sets sprinkled into Alexandrov subsets of Minkowski spacetime of dimensions 1+1, 1+2 and 1+3. In particular we consider the rank 2 past of sprinkled causet events, which is the set of events that are two links to the past. Assigning one of the rank 2 past events as ’preferred past’ for each event yields a ’preferred past structure,’ which was recently proposed as the basis for a causal set d’Alembertian. We test six criteria for selecting rank 2 past subsets. One criterion performs particularly well at uniquely selecting — with very high probability — a preferred past satisfying desirable properties. The second part of the paper concerns (infinite) sprinkled causal sets for general spacetime manifolds. After reviewing the construction of the sprinkling process with the Poisson measure, we consider various specific applications. Among other things, we compute the probability of obtaining a sprinkled causal set of a given isomorphism class by combinatorial means, using a correspondence between causal sets in Alexandrov subsets of 1+1 dimensional Minkowski spacetime and 2D-orders. These methods are also used to compute the expected size of the past infinity as a proportion of the total size of a sprinkled causal set.
@article{FewsterHawkinsMinzRejzner:2021, author = {Fewster, Christopher J. and Hawkins, Eli and Minz, Christoph and Rejzner, Kasia}, title = {{Local structure of sprinkled causal sets}}, eprint = {2011.02965}, archiveprefix = {arXiv}, primaryclass = {gr-qc}, doi = {10.1103/PhysRevD.103.086020}, journal = {Phys. Rev. D}, volume = {103}, number = {8}, pages = {086020}, month = aug, year = {2021}, }
2020
- causetsChristoph MinzNov 2020LaTeX-package to draw causal set (Hasse) diagrams.
This LaTeX package uses TikZ to generate (Hasse) diagrams for causal sets (causets) to be used inline with text or in mathematical expressions. The macros can also be used in the tikzpicture environment to annotate or modify a diagram, as shown with some examples in the documentation.
@misc{Minz:2020, author = {Minz, Christoph}, title = {{causets}}, month = nov, year = {2020}, note = {LaTeX-package to draw causal set (Hasse) diagrams.}, }
2016
- Shock wave polarizations and optical metrics in the Born and the Born-Infeld electrodynamicsAnn. Phys., Jan 2016
We analyze the behavior of shock waves in nonlinear theories of electrodynamics. For this, by use of generalized Hadamard step functions of increasing order, the electromagnetic potential is developed in a series expansion near the shock wave front. This brings about a corresponding expansion of the respective electromagnetic field equations which allows for deriving relations that determine the jump coefficients in the expansion series of the potential. We compute the components of a suitable gauge-normalized version of the jump coefficients given for a prescribed tetrad compatible with the shock front foliation. The solution of the first-order jump relations shows that, in contrast to linear Maxwell’s electrodynamics, in general the propagation of shock waves in nonlinear theories is governed by optical metrics and polarization conditions describing the propagation of two differently polarized waves (leading to a possible appearance of birefringence). In detail, shock waves are analyzed in the Born and Born-Infeld theories verifying that the Born-Infeld model exhibits no birefringence and the Born model does. The obtained results are compared to those ones found in literature. New results for the polarization of the two different waves are derived for Born-type electrodynamics.
@article{MinzVonBorzeszkowskiChrobokSchellstede:2016, author = {Minz, Christoph and {von Borzeszkowski}, Horst-Heino and Chrobok, Thoralf and Schellstede, Gerold}, title = {{Shock wave polarizations and optical metrics in the Born and the Born-Infeld electrodynamics}}, eprint = {1411.3163}, archiveprefix = {arXiv}, primaryclass = {math-ph}, doi = {10.1016/j.aop.2015.11.005}, journal = {Ann. Phys.}, volume = {364}, pages = {248--260}, month = jan, year = {2016}, }